Understanding living systems
Table of Contents
Tissue Physiology and Biophysics
Bronchial thermoplasty modelling
(with Bindi Brook & AirPROM consortium)
We are working on theoretical and experimental models which underpin Bronchial Thermoplasty (BT) treatment (application of electro-generated heat from within airways) for severe asthma. We aim to capture all the scales from cells to the entire lung to understand the impact of the treatment on lung structure and function. The combined modelling approach will allow better targeting of patient groups that could benefit most from the BT procedure, while also suggesting treatment protocol optimisation. Please see more details on AirPROM.
Growth dynamics of airway smooth muscle cells driven by stochastic inflammation
(with Bindi Brook & Oliver Jensen)
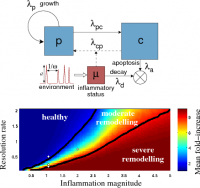 The project aims to quantify the uncertainty in the long-term severity of structural changes (remodelling) of an airway wall in asthma due to inflammation-driven smooth muscle mass accumulation. Inflammation is described as a temporal stochastic process, driven by a series of random inflammatory stimuli, which is coupled to a population growth model. In the paper with Brook et al. (PLoS ONE 2014), we have demonstrated, by means of asymptotic techniques and Monte-Carlo simulations, the strong impact of the inflammation resolution rate both on the expected long-term outcome and on the prediction uncertainty.
The project aims to quantify the uncertainty in the long-term severity of structural changes (remodelling) of an airway wall in asthma due to inflammation-driven smooth muscle mass accumulation. Inflammation is described as a temporal stochastic process, driven by a series of random inflammatory stimuli, which is coupled to a population growth model. In the paper with Brook et al. (PLoS ONE 2014), we have demonstrated, by means of asymptotic techniques and Monte-Carlo simulations, the strong impact of the inflammation resolution rate both on the expected long-term outcome and on the prediction uncertainty.
- The role of inflammation resolution speed in airway smooth muscle mass accumulation in asthma: insight from a theoretical model by Igor L. Chernyavsky, Huguette Croisier, Lloyd A. C. Chapman, Laura S. Kimpton, Jonathan E. Hiorns, Bindi S. Brook, Oliver E. Jensen, Charlotte K. Billington, Ian P. Hall, Simon R. Johnson (2014); PLoS ONE 9(3), pp. e90162. doi url preprint
Maternal blood flow and solute transport in the human placenta
(with Oliver Jensen, Lopa Leach and Ian Dryden)
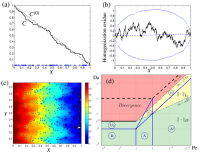 The paper with Jensen and Leach (Placenta 2010) aimed to bridge the gap between solute uptake kinetics and haemodynamics in the human placenta, employing the theory of porous media. Our results indicated the existence of an optimal density for fetal villous tissue and explained the critical role of the calibre of maternal decidual vessels.
The paper with Jensen and Leach (Placenta 2010) aimed to bridge the gap between solute uptake kinetics and haemodynamics in the human placenta, employing the theory of porous media. Our results indicated the existence of an optimal density for fetal villous tissue and explained the critical role of the calibre of maternal decidual vessels.
In the paper with Leach, Dryden and Jensen (Phil. Trans. Royal Soc. A 2011) we have addressed the effective macroscopic description of solute transport across multiple scales in regular and irregular geometries (e.g. arrays of point sinks), exploring possible transport regimes and the accuracy of an averaged description of the underlying stochastic microstructure. The invited follow-up paper with Dryden and Jensen (IMA J. Appl. Math. 2012) has shown a surprisingly strong dependence of the solute fluctuations on the global boundary conditions in some but not all parameter regimes. A novel analytical technique, verified by Monte-Carlo simulations, has been used to relate the corrector to an averaged description (homogenization residue) and the Brownian motion and to characterise its covariance function. These results open several interesting avenues of research that warrant further study.
Mechano-sensitivity and Adaptation
Intracellular and extracellular mechanics of a growing pollen tube
(with Anja Geitman, Anwesha Fernandes, Oliver Larkin and Richard Hill)
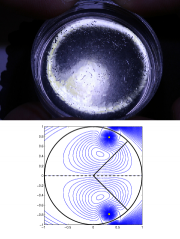 We have been studying the coupling of active and passive transport of microscopic vesicles critical for the cell growth, using the rapidly growing (up to 1 cm/h) pollen tube as a model system. In the study with Geitmann et al. (Nottingham 2010), we have shown the impact of the cell geometry and the rate of active transport by cytoskeletal network on the distribution of the vesicles. This problem has been further pursued theoretically and experimentally in Cambridge at the Ray Goldstein's biophysical lab (Cambridge 2012), and the work to understand the response of a growing cell to external fields and mechanical stresses continues, in collaboration with the strong magnetic field group of Laurence Eaves in Nottingham.
We have been studying the coupling of active and passive transport of microscopic vesicles critical for the cell growth, using the rapidly growing (up to 1 cm/h) pollen tube as a model system. In the study with Geitmann et al. (Nottingham 2010), we have shown the impact of the cell geometry and the rate of active transport by cytoskeletal network on the distribution of the vesicles. This problem has been further pursued theoretically and experimentally in Cambridge at the Ray Goldstein's biophysical lab (Cambridge 2012), and the work to understand the response of a growing cell to external fields and mechanical stresses continues, in collaboration with the strong magnetic field group of Laurence Eaves in Nottingham.
- Intracellular dynamics of secretory vesicles in the tip of growing pollen tubes by L. R. Band, I. L. Chernyavsky, R. J. Dyson, F. Z. Nouri, B. Piette, A. Geitmann (2010); Nottingham. url
Shear stress-sensitivity of endothelium and nitric oxide-mediated regulatory feedback
(with Nikolai Kudryashov)
The purpose of the paper with Kudryashov (Fluid Dyn. 2008) was to offer a new theoretical model that couples dynamically the fluid shear stress and muscle tone regulation in blood vessels via a biochemical feedback. The model describes how an artery adapts to changing flow conditions and predicts different oscillatory regimes. In particular, the vascular wall damping factor is shown to be a bifurcation factor. Our model explained the main features of relevant experiments, and we obtained an estimate for the oscillation frequency that captures both mechanical and biochemical vascular wall properties.
Pressure waves in viscoelastic vessels
(with Nikolai Kudryashov and Dmitri Sinelshchikov)
In the paper with Kudryashov (Fluid Dyn. 2006), we obtained a set of effective evolution equations for small-but-finite-amplitude nonlinear waves in a viscoelastic tube that account for various structural components of a blood vessel. Wall viscosity was shown to be important for damping the high-frequency oscillations. In addition, we suggested a classification of different vascular mechanical parameters with respect to dominating spatio-temporal scales.


